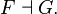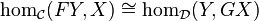commençons notre « examen »de la pensée mathématicienne, à propos de l’Un et de l’Etre, de la manière la plus « simple » possible , qui est aussi celle suivie par Badiou dans « L’Etre et l’évènement » : la théorie des ensembles.
Nous pouvons adopter la même attitude que Badiou au début de « L’être et l’évènement » pour éviter le supplice pervers de « tourner indéfiniment » dans le tourniquet des hypothèses du « Parménide » :
L’UN n’est pas
seulement en traduisant ceci, selon ce dont nosu avons convenu dans l’article précédent, en :
la pensée selon l’Un n’est pas la pensée selon l’être
méditer la question de l’être mène irrémédialbement au multiple, à l’autre que l’UN, à travers les étants, qui se disent de plusieurs façons, comme au début de l’Introduction à la métaphysique de Heidegger.
Un oiseau, un animal, un être vivant, ou bien une chose fabriquée, ou une pierre, ou un signe, ou un symbole, tout cela EST : l’Etre est l’autre que l’UN, l’ontologie est donc forcément la science du multiple pur, en cela Badiou a raison.
Dans la théorie des ensembles, le multiple, ce sont les éléments d’un ensemble :
x ∈ A
y ∈ A
etc.. : x et y sont éléments de l’ensemble A
dans la théorie pure, axiomatique , des ensembles, x et y sont à leur tour des ensembles, il n’y a pas d’éléments de base, de niveau zéro, puisqu’il n’y a qu’une seule notion, celel d’ensemble
http://en.wikipedia.org/wiki/Set_theory
Badiou enchaîne, comme on le sait , par :
l’UN n’est pas, mais il y a de l’un, ou encore : l’ un est le « compte-pour-un » qui enchaîne les éléments d’un ensemble à former une collection, un tout : cet ensemble justement
Un autre multiple qui apparaît est ce que Badiou appelle la représentation,à savoir l’ensemble des parties d’un ensemble A, noté :
P(A)
un ensemble X est une partie de A, ou un sous-ensemble de A :
X ⊆ A
si tout élément de X est élément de A :
x ∈ X implique x ∈ A
le multiple est donc dans la présentation (les éléments) ou la représentation (les parties, les sous-ensembles) d’un ensemble : penser selon l’être dans la théorie, ou la catégorie, des ensembles, c’est penser la présentation des éléments et la représentation des parties.
penser selon l’un, c’est penser le compte-pour-un qui fait que l’ensemble A est un ensemble « regroupant », ou « contenant » ses éléments, et ses parties.
Mais bien entendu, l’UN ne pourra être un ensemble, même l’ensemble de tout, c’est à dire en théorie des ensembles l’ensemble de tous les ensembles : car il est possible de démontrer facilement , à partir des paradoxes comme celui de Russell , qu’un tel ensemble est une notion inconsistante.
Formons en effet le concept des « ensembles qui ne s’appartiennent pas à eux mêmes, qui ne sont pas élément d’eux mêmes ».
C’est une notion apparemment évidente, et il faudrait ramer beaucoup pour trouver un ensemble qui est élément de lui même, et ce genre de notion est proscrit par toutes les théories « normales ».
Mais pouvons nous former la notion d’ensemble de tous ces ensembles qui ne sont pas éléments d’eux mêmes ?
appelons X cet hypothétique ensemble , de deux choses l’une :
-soit il ne s’appartient pas à lui même, mais alors il est un ensemble qui ne s’appartient pas à lui même, il est donc un élément de l’ensemble des ensembles qui ne s’appartiennent pas à eux mêmes, donc il est élément de l’ensemble de ces ensembles, qui est justement lui même, X , c’est à dire pour résumer :
si X n’est pas élément de X, alors X est élément de X
– soit il s’appartient à lui même, X est élément de X, mais alors il n’est pas un ensemble qui ne s’appartient pas à lui même, donc il n’est pas élément de l’ensemble de tels ensembles, qui est X, ou encore :
si X est élément de X, alors X n’est pas élément de X
dans les deux cas, nous aboutissons à une contradiction !
Nous pourrions dire que cette démonstration « formalise justement mathématiquement » la proposition philosophique que l’UN n’est pas.
L’Etre, ou les êtres, ce sont les éléments, qui sont toujours des ensembles.
La pensée selon l’un, c’est le compte-pour-un qui fait « tenir ensemble » les éléments d’un ensemble.
L’UN, ce serait , si l’UN était, un ensemble, l’ensemble de tous les ensembles, seulement c’est une notion incosistante, conclusion :
l’UN n’est pas.
Seulement cette démonstration s’appuie sur le fait, propre aux universels abstraits, qu’un ensemble, regroupant des objets ayant une propriété, n’a pas lui même cette propriété. Si l’universel est l’ensemble qui fait tenir ensemble ses éléments, alors cet universel est transcendant à ses « singuliers », les éléments, et à ses « particuliers », ses parties.
Or il existe une autre notion d’universel que celui de la notion ensembliste : c’est la pensée de l’universel concret, obtenue à partir de la théorie des catégories, comme on le voit dans les travaux de David Ellerman que j’ai commenté ici :
http://apodictiquemessianique.wordpress.com/universalisme-abstrait-et-concret/
http://mathesis.blogg.org/page-universalisme_abstrait_ensembliste_et_universalisme_concret_fonctoriel-747.html
http://www.ellerman.org/Davids-Stuff/Maths/Conc-Univ.pdf
« Dans la théorie platonicienne des Idées ou formes (Eidê), toute propriété F donne lieu, est associée à un universel uF qui la représente de manière unique.
Un objet x a la propriété F si et seulement s’il « participe » à l’universel uF : F(x) ↔ x μ uF ( μ comme « metexis » est le signe de « participer ») (condition d’universalité)
Une théorie mathématique des universaux doit, en plus de cette relation binaire μ être munie d’une relation d’équivalence (cad réflexive , symmétrique et transitive) ≈ telle que l’on ait la condition d’unicité, ou plutôt d’isomorphisme :
si uF et u’F sont deux universaux associés à la même propriété F alors on doit avoir : uF ≈ u’F (condition d’unicité)
Un universel est dit abstrait s’il ne participe pas à lui même : ¬ ( uF μ uF )
Il est dit concret s’il participe à lui même : uF μ uF
On trouve dans la philosophie, et notamment chez Platon, des universaux des deux espèces, abstraits et concrets. Nous travaillerons ici à faire descendre Platon du Ciel en Terre, dans le même mouvement selon lequel Copernic avait projeté la Terre dans le Ciel : ce qui veut dire ne se soucier que des universaux concrets, à portée d’expérience et de pensée humaine, et « oublier » les formes existant « séparément », dans un monde Intelligible qui ne veut rien dire pour nous. Telle est la leçon que nous retenons de Brunschvicg et de sa réinterprétation de l’idéalisme platonicien (à la suite de Kant) et du pythagorisme (voir là dessus les deux articles à propos de « Spiritualisme et sens commun »).
Or deux théories très générales se présentent à nous en mathématiques, très différentes de par la « relation de participation » qu’elles proposent :
– la théorie des ensembles, où la relation de participation μ est la relation d’appartenance à un ensemble : ∈ ; x participe à B si et seulement si x appartient, ou est un élément, de l’ensemble B : x ∈ B
– et la théorie des catégories, où la relation de participation proposée par ellerman est celle de « factorisation unique par un morphisme », intervenant fréquemment pour définir une « construction universelle » (exemple : le produit tensoriel classique d’espaces vectoriels) :
x participe à y si x,y sont objets d’une catégorie C et s’il existe un morphisme unique μ dirigé de x vers y :
μ : x → y
Or les universaux ensemblistes sont abstraits, car le paradoxe de Russell a encouragé les mathématiciens à éliminer les ensembles qui s’appartiennent à eux mêmes (Badiou les retient dans l’Etre et l’évènement pour formaliser l’évènement justement, soit ce qui n’appartient pas à l’ontologie mathématique « normale » : l’évènement est une rupture du « normal »). »
Nous venons de voir plus haut, à partir du paradoxe de Russell, que dans la pensée ensembliste, qui est un « modèle mathématique » de la pensée selon l’être, de ce qui correspond à l’ontologie dans notre shcéma idéaliste, les universels, les ensembles, ne peuvent être qu’abstraits.
Mais dans la théorie des catégories, qui est un modèle, LE modèle mathématique de ce que nous appelons pensée selon l’un, les universels sont tous concrets, puisqu’un des seuls axiomes de cette théorie est que pour tout objet Y d’une caégorie, il existe toujours un morphisme identité :
« Dans la théorie des catégories, la forme même de la condition d’universalité de la participation μ : x → y
fait que tout universel y est toujours concret. Ceci est garanti parun des axiomes de la théorie, qui est l’existence d’un morphisme identité Idu pour tout objet u :
Idy : y → y«
conclusion : dans ce type de pensée, qui est supérieure à la pensée ensembliste, comme en conviennent les mathématiciens modernes qui ont remplacé la théorie des ensembles (encore retenue par Bourbaki) par la théorie des catégories pour fonder les mathématiques , les thèses de Badiou , opposant un « évènement » modélisé par un ensemble anormal, s’appartenant à lui même, et donc proscrit par l’ontologie, à l’être des ensembles normaux, ces thèses s’effondrent.
Car dans la théorie des catégories, tous les universels sont concrets , il n’y a, en somme, que des évènements !
Ce n’est guère étonnant, puisque la pensée catégorie part des morphismes, c’est à dire des transformations, de ce qui forme la substance du changement.
Un évènement est quelque chose qui arrive, un changement : dans la pensée selon l’un, il n’y a que des changements, des évènements, qui arrivent…