Article venant à la suite de :
David Ellerman : concrete universals in category theory
Où nous étudions de près le travail de Divic Ellerman: « Concrete universals in category theory »
Cliquer pour accéder à Conc-Univ.pdf
À partir de la fin de la page 2 de cet article David Ellerman se penche sur la theorie des ensembles dont l’idée originale fondatrice était selon lui de former une théorie générale des universaux , un universel étant accolé à une propriété sous la forme d’une entité telle que tout objet possédant la propriété en question aurait une relation spéciale avec cette entité. La théorie des ensembles propose comme relation la relation d’appartenance de la theorie des ensembles notée par le signe ∊et comme « entité universelle » accolée à une certaine propriété P l’ensemble de tous les objets ayant la propriété P.
Seulement Bertrand Russell trouva un paradoxe qui met à mal cette théorie , il examina la propriété P des ensembles consistant pour un ensemble à « ne pas être élément de lui même « :
Un ensemble X possède la propriete P s et seulement si (ssi) X ∉ X ( X n’appartient pas à X ), X n’est pas élément de X). Soit alors l’entité universelle Z accolée à cet propriété P, c’est à dire l’ensemble de tous les ensembles qui ne s’appartiennent pas à eux mêmes .
Demandons nous si Z appartient à lui même ou non.Nous nous heurtons à un paradoxe logique le paradoxe de Russell:
Si Z appartient à Z : Z ∊ Z alors Z appartient à l’ensemble de tous les ensembles qui ne s’appartiennent pas à eux mêmes, donc il ne s’appartient pas à lui même. Dons si Z appartient à lui même alors Z ne s’appartient pas à lui mêmes : contradiction !!!
Et dans le cas alternatif si Z n’appartient pas à lui même : Z ∉Z, alors Z n’a pas la propriété P » être un ensemble qui ne s’appartient pas à lui même) donc il s’appartient à lui même puisqu’il est faus de dire qu’il ne s’appartient pas à lui meme. Don si Z ne s’appartient pas à lui même alors Z s’appartient à lui même. Contradiction encore !!!
Donc dans les deux cas de l’alternative ( soit Z appartient à Z soit Z n’appartient pas à Z c’est soit l’un soit l’autre) nous nous heurtons à une contradiction, cela signifie que la théorie consistant à associer à toute propriete P un universel abstrait : ensemble de tous les éléments ayant cette proprété , que cette theorie donc est fausse parce qu’elle aboutit à un paradoxe . il y a deux manières d’éviter ce paradoxe : soit par la théorie des types :
https://fr.m.wikipedia.org/wiki/Théorie_des_types
Soit par la théorie NBG des classes de Von Neumann-Bernays-Godel :
https://fr.m.wikipedia.org/wiki/Théorie_des_ensembles_de_von_Neumann-Bernays-Gödel
Intuitivement parlant les classes sont des multiplicités » plus grandes » que les ensembles .Une classe ne peut être élément d’un ensemble ou bien d’une autre classe . toute classe correspond à une propriete selon le schémaexpliqué plus haut de l’entité universelle de tous les objets possédant une propriété P .
À toute propriete P des ensembles ( des étants multiples qui sont des ensembles puisque la theorie des ensembles est l’ontologie, comme l’a démontré’ Alain Badiou dans « L’être et l’événement »)correspond une classe et réciproquement : la classe des ensembles ayant cette propriété P.
La collection de tous les ensembles ne s’appartenznt pas à eux même est intuitivement « trop grande » pour être un ensemble, c’est donc une classe quelque chose de plus grand que tout ensemble . Essayez de former un ensemble qui s’appartient à lui même , vous aurez du mal : on n’en trouve pas dans la vie quotidienne , ainsi l’ensemble de ces cinq pommes dans la corbeille n’est pas élément de lui même quel sens cela aurai il ? Les éléments de cet ensemble ce sont chacune des cinq pommes et rien d’autre..
Pour penser des ensembles qui sont éléments d’eux mêmes il faut faire travailler ses méninges : on y arrive par des tours de passe passe , par exemple en considérant les ensembles qui ont la propriete de pouvoir être caractérisés par une phrase en francais de moins de x lettre, x étant un nombre entier que nous calculerons de manière à retomber sur nos pattes , considérons en effet l’ensemble de tous les ensembles ayant cette propriété, il peut être décrit en francais par la phrase suivante :
Z = « Ensemble de tous les ensembles pouvant être décrits par une phrase en Français de moins de x lettres ou chiffres «
Cette phrase a 93 ( si j’ai bien compté) lettres ou chiffres donc en prenant x = 95 ( car x a deux chiffres donc remplacer x par deux chiffres dans la phrase ci dessus portera le nombre de caractères à 94) nous sommes rendus et pouvons dire que l’ensemble Z appartient à lui même puisque sa définition en langue française nécessité 94 caractères donc moins de 95 caractères , lettres ou chiffres.
On a un peu le sentiment d’assister à un tour du Bateleur

Donc il est très difficile de former des ensembles s’appartenant à eux mêmes ce qui veut dire que « presque tous les ensembles ne s’appartiennent pas à eux mêmes donc la collection de tous les ensembles ne s’appartenant pas à eux mêmes est « trop grande » pour être un ensemble elle est donc une classe. Il en va de même de la collection de « tous les ensembles », ce n’est pas un ensemble mais une classe, la classe de « toutes les multiplicités ayant la propriété d’être un ensemble » n’est pas un ensemble mais une multiplicité plus grande qu’un ensemble ( puiqu’elle contient les ensembles ne s’appartenant pas à eux mêmes vu qu’elle contient tous les ensembles). C’est une classe, la classe de tous les ensembles, « trop grande »pour être un ensemble.
Et la propriete d’être une classe? Quelle multiplicité , celle de toutes les classes, lui correspond? Pas une classe puisqu’aucune classe ne peut appartenir à une autre.
C’est un conglomérat, le conglomérat de toutes les classes.
Une classe ne peut pas être élément d’un ensemble ni d’une autre classe, mais elle peut être élément d’un conglomérat.
Voit là dessus:
Cliquer pour accéder à Proseminar2014_Vortrag01.pdf
Ces theories des différents ordres de multiplicités intéressent au plus haut point les mathematicinens catégoriciens et par eux les philosophes .Il est vrai que la theorie se pose rarement ce genre de questions t butte rarement sur des paradoxes aussi embêtants que la theorie des ensembles : c’est qu’elle a comme intégré ces différentes sortes de multiplicités par l’intermédiaire des collections des objets ou DES morphisme sur d’une catégorie quelconque , sui peuvent être des ensembles ou des classes , voire éventuellement des conglomérats , auxquels cas respectifs la catégorie est dite petite ou grande ( en anglais : , »large »).voir par exemple cette page du Nlab sur les » large categories »:
http://ncatlab.org/nlab/show/large+category
Ainsi que cette note où les conglomérats, classes , ensembles sont abordés, ainsi que les univers de Grothendieck qui en sont une alternative ( ce géniedémiurgique à la Orson Welles fut vraiment un créateur d’Univers et des théories comme le philosophe selon Deleuze est « créateur de concepts »:
Cliquer pour accéder à FoundationsForCategoryTheory.pdf
Apprenez y aussi ce que c’est en logique qu’une théorie du premier ordre ( « firstt order theory »)
Notion importante pour la suite de ce blog qui s’intéressera de plus en plus la logique à la fois philosophique et mathématique ( fondée largement sur les topos) , nonobstant le mépris que lui témoigne Brunschvicg et dont a hérité Badiou son disciple infidèle et cachottier (il ne nomme jamais Brunschvicg cela lui écorcherait sans doute la langue).
Si l’ontologie théorie de l’Etre envisagé dans sa dimension de multiple pur est la theorie des ensembles ( thèse incontournable de Badiou ) alors les étants sont les ensembles et les propriétés d’étants sont les classes. .les catégories sont situées au carrefour de ces deux dominés ou voies ( étants et leurs propriétés ) qui constituent ce que nous appellerons le plan ontique dont l’accès est facilité voire permis à l’esprit humain par ces verres grossissants que sont la théorie des ensembles ou des classes.
Les lecteurs attentifs au mouvement des idées ne manqueront pas de remarquer dans le texte de David Ellerman l’opposition claire tracée entre la théorie des ensembles qui est celle des universaux abstraits et la theorie des categories qui traite des universaux concrets .Je me suis inspiré de cette double notion d’universalité dans la pègre suivante recopiée sur plusieurs blogs :
Deux universalismes : concret-catégorique-hénologique et abstrait-ensembliste-ontologique
Selon Ellerman et je l’approuve entièrement, la theorie des categories est tout simplement une version mathématisée de la théorie platonicienne des Formes (Idées) qui est le coeur et la profondeur spirituelle du platonisme et donc de toute la philosophie s’il est vrai, comme le dit Brunschvicg que » le platonisme est la vérité de la philosophie » ou, comme le dit Whitehead, que « toute la philosophie occidentale ( c’est à dire, c’est moi qui précise, toute la philosophie) se réduit à des notes en bas de pages des ouvrages de Platon ».
Selon Ellerman (page3 de l’article) la théorie des catégoriesest le cadre mathématique qui permet de reconnaître les « universaux concrets » des mathématiques, c’est à dire les exemples concrets qui exemplifient de manière parfaite une propriété mathématique. Dans le cas où un dieu-démiurge s’inspirerait dune Idée préxistante du Cheval, comme le croient les conceptions naïves du platonisme,alors que l’universel abstrait serait l’en semble de tous les chevaux (mais un tel universel évoluerait avec le temps et l’apparition incessante de nouveaux chevaux ) un tel universel concret associé à l’Idée du Cheval serait un cheval absolument parfait en beauté en force et en vitesse et surtout représentant parfaitement ce qu’est l’essence même du cheval mais comment reconnaître ce genre de perfection ? il faudrait entrer dans l’esprit du Dieu prééxistant au démiurge qui a formé une telle Idée ou de ce qu’il est devenu en mentalité judéo-islamochrétienne, à savoir le Dieu Créateur de l’Universmais comment cela serait il possible à une créature imparfaite telle qu’une être humain ? c’est pourquoi il vaut mieux limiter les Idées au domaine mathématique créé par l’intellect humain , où l’être humain peut reconnaître un telle perfection dans l’exemplification d’une propriété mathématique et donc un universel concret …
Ellerman formalise ainsi la théorie platonicienne des Formes page 4 : à toute propriété F est associée un universel uF
Il ya aussi une relation de participation notée μ (comme μεθεξις = « participation) :
un objet x participe à l’universel est noté en langage formel ; x μ u F
en renversant les choses, etant donné une propriété Fet une relation μ , une entité uF est dite universelle pour F (relativement à μ) si elle respecte la condition dite d’universalité :
pour tout objet x: x μ uF si et seulement si F(x) (ce qui veut dire x a la propriété F)
Cette condition d’universalité est accompagnée ,pour la définition d’un universel , de la condition d’unicité(à une équivalence près ) voir page 4 de l’article de David Ellerman , condition qui s’énonce ainsi :
Si uFet vF sont deux universels (c’est à dire satisfont à la condition d’universalité ci dessus) pour la même propriété F ils doivent être équivalents : uF ≊ vF
(une th »orie mathématique doit, pour être une théorie des universaux , posséder une relation d’équivalence ≊ et une relation de participation μ telle que ci dessus afin de pouvoir définir les deux conditions cidessus d’universalité et d’unicité à une équivalence près.
Dans la théorie des catégories comme dans la théorie des ensembles la relation d’équivalence sera l’isomorphisme qui est cependant défini plus simplement dans la théorie des catégories où un isomorphisme est défini comme un morphisme inversible c’st à dire un morphisme m muni d’un morphisme inverse i tel que , si ° est l’opération de composition des morphismes et si la flèche m va de l’objet A à l’objet B et i va de B à A:
m : A → B
i : B → A
alors : m°i = IdB : B → B (morphisme identité sur B)
et i°m = IdA : A → A (morphisme identité sur A)
Dans la théorie des ensembles les deux ensembles A et B sontdits isomorphes s’il existe une application bijective (c’est à dire à la fois injective et surjective) de A vers B c’est à dire si, dans le cas où ils ont tous deux un nombre fini d’éléments, s’ils ont le même nombre d’éléments .
voir :
https://fr.wikipedia.org/wiki/Bijection
on vérifie facilement qu’une application bijective entre deux ensembles est inversible.
Dans le cas de la théorie des ensembles la relation de participation μ est la relation d’appartenance (« elementhood ») d’un élément à l’ensemble dont il est un élément, relation notée ∈. Ce n’est pas une relation symétrique car si A ∈ B ,il n’est pas vrai en général que B ∈ A Elle n’est pas non plus transitive car si A ∈ B et si B ∈ C il n’est pas vrai en général que A ∈ C
Dans la théorie desz catégories la relation de participation μ est la relation de « factorisation unique » c’est à dire que u participe à v s’il existe un morphisme unique f allant de u vers v :
∃! f : u → v
le point d’exclamation accolé au signe logique ∃ qui signifie « il existe » veut dire l’unicité « il existe un unique morphisme f »)
voir nos articles
https://meditationesdeprimaphilosophia.wordpress.com/2015/08/12/propriete-universelle-en-theorie-des-categories/
et
https://mathesisuniversalis2.wordpress.com/2015/08/15/quest-ce-quune-propriete-universelle-y-a-til-une-reponse-satisfaisante/
Une limite d’un cône en théorie des catégories est l’exemple même d’un universel : la relation de participation se situe dans l’existence d’un morphisme unisque rendant commutatif un diagramme voir :
https://fr.wikipedia.org/wiki/Limite_(th%C3%A9orie_des_cat%C3%A9gories)
« Soit C une catégorie. On considère un diagramme (en) dans C, traduit par un foncteur F : D^{\mathrm{op}} \to C1. Dans de nombreux cas, on considère D une petite catégorie, voire finie, et on parle respectivement de petit diagramme ou de diagramme fini.
Un cône (en) dans F est la donnée d’un objet N de C et d’une famille \psi_X: N \to F(X) de morphismes indicés par les objets X de D^{\mathrm{op}}, telle que pour tout morphisme f : X → Y dans D^{\mathrm{op}}, on a F(f) \circ \psi_X = \psi_Y. Une limite du diagramme F : D^{\mathrm{op}} \to C est un cône (L, \phi) dans F tel que, pour tout autre cône (N, \psi) dans F, il existe un unique morphisme médiateur u : N → L vérifiant \phi_X \circ u = \psi_X pour tout X dans D^{\mathrm{op}}. Ainsi, tout cône se factorise par la limite, de manière unique. En d’autres termes, on a le diagramme suivant : »

et comme nous l’avons déjà vu, des exemples classiques de limites sont le produit (qui dans le cas de la catégorie des ensembles est le produit cartésien de deux ensembles) , l’exponentiele, le « produit fibré » (en anglais « pullback ») , ou même l’objet initial (qui est limite d’un diagramme vide ) ou leurs notions duales ,en renversant le sens des flèches, appelées colimites : coproduit ou somme, coproduit fibré (en anglais « pushout ») ou objet terminal comme notion duale de celle de l’objet initial.
Voir par exemple cet article de moi qui fait le lien avec les théories de Wronski sur les « algorithmas primitifs » (addition, multiplication exponentiation ):
https://henosophiamathesis.wordpress.com/2015/08/29/exponentielle-somme-et-produit-comme-limites-de-diagrammes-en-theorie-des-categories/
On compren mieux avec ces exemples ce que veut dire l’affirmation d’Ellerman suivant laquelle la relation de participation à un universel eest en théorie des catégories la relation de factorisation selon un morphisme unique : x participe à u, noté : x μ u si et seulement s’il existe une flèche unique de x vers u (on dite : « factorisation unique de x par u »)
∃! f : x → u
On voit bien alors qu’en théorie des catégories n’importe quel universel participe à lui même car il existe toujours un morphisme identité :
Idu : u → u
Ceci se dit : la relation de participation est réflexive ‘tout universel participe à lui même
et ce morphisme doit être unique parce que la relation de factorisation par u concerne n’importe quelle flèche partant de x vers un autre objet que u , ce qu’Ellerman ne précise pas car ce n’est pas le sujet mais que l’on voir dans les pages Wiki consacrées à la notion de limite en théorie des catégories
une flèche g : x → w se factorise par u signifie qu’elle est la composée de la flèche unique f ci dessus par une autre h allant de u vers w c’est un exemple de diagramme commutatif :
g = h°f : f : x → u suivie de h : u → w
dans le cas où x = u, f ne peut être que Idu
De même comme les morphismes se composent et que les morphismes identité sont « éléments neutres » pour cette loi de composition , on voit que la relation de participation est transitive dans le cas de la théorie des catégories : si x participe à u et u participe à w alors x participe à w (laflèche composée de deux morphismes identité reste un morphisme identité)
Dans le cas de la théorie des ensembles où la relation de participation est la relation d’appartenance ∈ , nous n’avons plus ces propriétés car cette relation n’est ni réflexive ni transitive.
Or Ellerman appelle « abstraits » les universaux qui ne peuvent participer à eux mêmes et concrets ceux qui participent à eux mêmes; on voit donc que la théorie des ensembles est celle des universaux abstraits, et la théorie des catégories celle des universaux concrets .
J’associe, ensuivant l’approche de Badiou selon lequel la théorie des ensembles est l’ontolgie la théorie des ensembles au plan ontique ou « plan d’être » ou « plan de transcendance « .
Et donc la théorie des catégories au plan d’immanence. J’ai bien insisté sur cette dualité ‘dualité de la phénoménalité dit Michel Henry ) dns la page que j’ai tirée de cet article d’Ellerman :
https://mathesisuniversalis2.wordpress.com/deux-universalismes-concret-categorique-henologique-et-abstrait-ensembliste-ontologique/
Le paradoxe de Russell a poussé les théoriciens à proscrire l’auto-appartenance pour les ensembles, c’est à dire à interdire la thèse A ∈ A pour tout ensemble A
Badiou le dit dans « l’Etre et l’évènement « dans son style célèbre et si reconnaissable :
« L’ontologie mathématicienne proscrit l’existence d’un ensemble s’appartenant à lui même, c’est à dire de l’évènement »
L’ontologie mathématicienne c’est selon lui la théorie des ensembles ZF, axiomaisée par Zermelo-Fraenkel, et il identifie le mathème de l’ensemble appartenant à lui même à ce qu’il appelle un « évènement » ainsi soit un évènement comme la « Révolution de 1789 »,il évoque un ensemble appartenant à lui même de par l’autoréférence incessante dont font preuve les révolutionnaires dans leurs discours , où ils font sans arreêt allusion au nom « la Révolution » . On pourrait ire la même chose de l’évènement-Christ , sans cesse nommé dans les écrits chrétiens , ou bien à l’incessante autoréférence coranique qui lui attire qulques ennuis d’ordre logicien de ma part :
https://meditationesdeprimaphilosophia.wordpress.com/demonstration-rigoureuse-de-limposture-du-coran/
Il existe un autre intedit formel de la mathématique, catégorique cette fois, concernant les catégories internes à une autre catégorie , notion que nous n’avons pas encore étudiée ici mais qui s’avère très importante , voir ces liens :
https://en.wikipedia.org/wiki/Internal_category
et sur le Nlab :
http://ncatlab.org/nlab/show/internal+category
ainsi que https://www.dmi.unict.it/ojs/index.php/lematematiche/article/viewFile/456/427
Je laisse à Badiou son interprétation d’un ensemnle élément de lui même comme évènement, façon subtile pour un philosophe de lémancipation de reconnaître l’existence d’un interdit tout en le contournant par un tour de passe passe langaier mais je mérite sans doute le même jugement sévère car je décèle le couple immanence/Transcendance dans la catégorie interne à une autre catégorie qui est la « catégorie ambiante » , la catégorie interne étant selon moi immanenteà l’autre qui est ainsi en position de Transcendance par rapport à elle .
Or l’interdit dont je parlais s’énonce (et se démontre) ainsi :
« Il ne peur exister une catégorie interne à elle même »
j’avais fait un article là dessus en recopiant un échange sur le mailing list des catégories :
https://mathesismessianisme.wordpress.com/2015/05/01/une-categorie-interne-a-elle-meme/
(en plus c’est de l’anglais et c’est présenté dans le fouillis des échanges sur un forum : si vous ne comprenez pas tout ce n’est pas grave, vous »êtes pas « Seul(e) sur Mars » mais sachez que l’interdit tient, et qu’il est reconnu par toute la communauté mathématicienne, ce qui possède à mon avis une signification un peu plus importante que l’interdiction du blasphème contre Dieu ou les Prophètes part toute la communauté des vrais croyants .
Peut on tracer cependant un parallèle entre ces deux interdits mathématiciens que nous venons de rencontrer (ensembliste et catégorique ) et d’autres interdits célèbres et universels ?
on le peut à mon avis avec , peut être, l’interdit de l’inceste qui est absolument universel et concerne tous les peuples de toutes religions mais dont on peine à trouver l’origine comme à donner la signification ou la justification (mises à part les justifications d’ordre génétiques ou le fait que « cela nous dégoûte », donc de l’ordre du plan vital ) : ne serait ce pas que l’enfant est d’abord (avant la naissance ) »contenu » dans le ventre de la mère ou bien , comme spermatozoîde » dans l’organisme du père et que le coït avec le père ou la mère (c’est là la sorte d’inceste qui nous horrifie vraiment) serait commeune rupture du couple immanence /transcendance dans le cas d’une catégorie interne à elle même ? vous trouvez certainement que je me hasarde ici dans le « no man’s land » du grand n’importe quoi et vous avez certainement raison mais sachez que je tiens à mon interprétation de l’interdit d’une catégorie interne à elle même comme interdit de la Transcendance car elle sert mes ténébreux desseins d’identifier le « plan d’immancne de Deleuze » au plan de l’Idée ou de la mathesis brunschvicgien ou « plan spirituel » , le plan vital étant le monde comme plan de la Transcendance ce que reconnaît aussi Michel Henry : ainsi se départagent les deux types d’attitude religieuse dont parle Jean Piaget, disciple de Brunschvicg , le premier type étant celui de l’immanence et le second celui de la Transcendance et ainsi les religions du Dieu Transcendant ne seraient pas si « nobles » que clla car elles consisteraient plus ou moins à faire chuter le ciel (plan spirituel ou plan d’immanence) sur la Terre (plan vital)
le second Interdit dont on peut faire le rapprochement concerneen physique le voyage temporel, et spécifiquement celui en direction du passé, objet de grands films comme « La jetée » de Chris Marker ou bien « L’armée de douze singes » de Terry gilliam qui en est adapté.
(je refuse de considérer les « Retour vers le futur » comme de grands films)
Si vous avez lu cet article jusqu’ici, et c’est le cas puisque vous êtes en train de lire cette phrase, vous avez sans nul doute le droit, en récompense de votre héroïsme, à cette petite récréation : le film « La jetée » de Chris Marker sur Youtube:
https://www.youtube.com/watch?v=zKW8kLGJYXg
Or on sait que Kurt Gödel, dont la folie des derniers temps(il s’est laisé mourir de faim car il craignait un complot consistant à empoisonner sa nourriture ) a été analysée dans un livre très intéressant « Les démons de Gödel« a rendu folles les équations de la Relativité générale d’ Einstein en leur permettant de donner naissance, par stricte dérivation logico-mathématique, à une « closed timelike curve » (CTC) ce qui est le nom scientifique d’une voyage ver e passé ; Gödel a imaginé un dispositif un peu étrange celui d’une immense roue se mettant à tourner très vite , au moins à la moitié de la vitesse de la lumière et montré par des calculs utilisant les équations de la Relativité générale qu’un homme attaché sur la roue ( bien attaché espérons le, d’ailleurs personne n’a pu certifier que ce » voyageur » pourrait survivre à de telles péripéties) remonterait dans le passé et qu’il pourrait s’approcher aussi près que souhaité de lui même dans le passé ou que n’importe lequel de ses ancêtres , lui permettant ainsi, s’il avit une mentalité un peu « révolutionnaire et terroriste » de tuer son double du passé (comme William Wilson dans le conte d’Edgar Poe) ou bien de tuer son papa , ou son grand père, ou bien sûr sa mère ou sa grand mère avec tous les effets paradoxaux que cela entraînerair pour sa propre existence(peut il exister alorsque ses parents sont morts avant d’avoir pu lui donner naissance ?) .
Des théoriciens aussi prestigieux que Hawking ont réfléchi sur ces paradoxes logiques du voyage dans le temps et pensé à une sorte de « conspiration cosmique » : le voageur temporel pourrait certes s’approcher de son père dnas le passé mais au moment de passer à l’acte contre le vénéravle papa des cinrconstances surviendraient qui lui interdiraient de le tuer ou même de le blesser ou d’influer sur sa ligne spatiotemporell : l’arme s’enrayerait comme par hasard, ou bien une tuile tomberait sur le voyageur,comme par hasard, l’empêchant de commettre son terrible acte terroriste, etc..etc..il me semble que Hawking appelle cela « cosmic censorship »
A la fin de « La jetée » ou de « L’armée des douze singes » qui en est tiré on assiste à un tel dispositif d’interdit mais réalis »é parun mystérieuse « Brigade du Temps » ou bien dans le film de Gilliam par les homme du futur qui ont envoyé Bruce Gillis dans le passé d’avant la catastrophe écologique et technoscientifique qui a exterminé presque toute l’humanité en 1997, mais lui entend rester dans ce passé de son enfance où l’on respire du si bon air (il y a aussi un femme là dessous, bien sûr, comme dans le film de Chris Marker, plan vital quand tu nous tiens !)et les hommes de l’avenir ne veulent pas qu’il se sépare ainsi de son (leur)temps …
bref j’ai un peu dérivé par rapport à cet admirable David Ellerman mais je tiens à dire que nous reviendrons encore un fois (au moins) sur cet article formidable car Ellerman y aborde l’adjonction à la fin à parit de la pge 14 ansi que sur l’inférence logique chère à Kurt Gödel page 12 ….

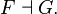
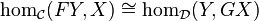



Vous devez être connecté pour poster un commentaire.